Students and Teachers Forum

1. If a+b+c =0, prove that
 1xb+c×1xc+a×1xa+b=1

.....

2. It is easy to open the lid of a can by using a spoon. Give reason.

.....

3. Iron cutting scissors have short cutting edges whereas cloth cutting scissors have long edges. Why?

.....

4. What is wedge? 
What is screw?

.....

5. What is an inclined plane?

.....

6. What is pulley? What is its function?

.....

7. In which class of lever is the effort arm always smaller than the load arm?

.....

8. If abc = 1, prove that:
 11+a+b-1+11+b+c-1+11+c+a-1=1

.....

9. What is lever? Give two examples.

.....

10. What will be the mass of body when 20 N of force is applied on it so that it produces an acceleration of 4 m/s2?

.....

11. How much force is required to produce an acceleration of 2 m/s2 on a car of mass 1000 kg?

.....

12. If 20N force is required to lift a 5 kg mass. Find the acceleration produced on the body.

.....

13. Find the acceleration of car, if its velocity increases from 20 m/s to 50 m/s in 5 seconds.

.....

14. A bus starts to move from the rest with an acceleration of 0.25 m/s2 . Find its final velocity after 3 minutes.

.....

15. Bina leaves home on a bicycle and reaches her school in 30 minutes. If the school is 25 km far from her home, calculate the average speed of her bicycle.

.....

16. Ram takes 2 minutes to cover a distance of 500 meter. Calculate his speed.

.....

17. In the given figure, ABCD is a cyclic quadrilateral. If ∡FAB = (x+20)⁰ and ∡BCE= (x-20)⁰, find the value of x.

.....

18. In the given figure, BC = 20cm ∡ABC = 30⁰ and area of ∆ABC is 75 cm2, find the length of AB.

Given, Area of △ABC = 75 cm2  CB = 20 cm AB = ?  Now, Area of △ABC = ( 1 / 2 ) x CB x AB x sinB or, 75 = ( 1 / 2 ) x 20 x AB x sin30o or, 150/20 = AB x ( 1 / 2 ) (∴ sin30o = 1/2) ∴ AB = 15 .....

19. Find the unknown angle:

.....

20. Find the unknown angle:

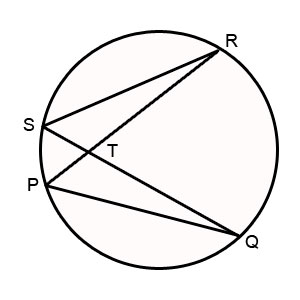
Here, ∡PSQ = ∡PRQ = 35o ( angles on the same arc PQ) ​​​​​​​∡PQR = 90o ( inscribed angle made by lines extending from diameter ) In △PRQ x + y + 90o =180o ( sum of interior angles of a triangle .....

21. Find the unknown angle:

In the given circle, Triangle COB is an isosceles triangle because OC = OB ( radius of the circle ) ∡CAB = ∡CDB = 65o ( angles of an isosceles triangle ) ∡CAB + ∡CDB + ∡COB = 180o ( sum of interior angles .....

22. Find the size of unknown angle in the following figures.

Here,  Exterior angle AOB + Interior angle AOB = 360o (complete angle) ∴  Exterior angle ∡AOB = 360o - 140o = 220o Now, ∡ACB = ( 1 / 2 ) of Exterior angle ∡AOB ( circumference angle is half of the centre .....

23. What kind of  object is said to be stationary and what kind of objects is said to be moving?

.....

24. If the veloctiy of a vehicle starting from rest reaches 5 m/s in 2 second, is the veloctiy of the vehicle uniform? Explain.

.....

25. In the given diagram, O is the centre of the circle and ABCD is a cyclic quadrilateral. If ∡ABC =65⁰ and ∡CED =75⁰, find the value of ∡DCE.


 

.....

26. A car starts from rest. If the acceleration of the car remains 2 m/s2 for 2 seconds, calculate the final velocity of the car. 

.....

27. In the given figure, O is the centre of circle. ∡XOY =50⁰, find the value of ∡XZY.

.....

28. In the given figure, AB =8cm and ∡APB =60⁰. PA and PB are tangents to the circle. Find the length of PA and PB.

Here,  PA = PB ( tangents to the circle originating from the same point are equal ) ∴△PAB is an isosceles triangle so, ∡PAB = ∡PBA = y In △PAB, ∡PAB + ∡PBA + ∡APB = 180o ( sum of interior .....

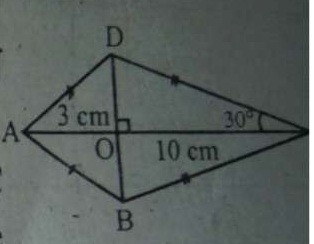
29. In the given figure, find the area of ∆DCE in which AB//DE, AD//BE, AB =8cm, DC = 8cm and ∡CDE = 30⁰.

Given, DC = 8 cm DE = 8 cm  ∡CDE = 30o ∴ Area of triangle DCE = ( 1 / 2 ) x DC x DE x sin(∡CDE)                                       .....

30. If a car travels 5 km in 5 minutes, what distance does it travels in 1 second?

.....

31. Find the value of x and y of the circle.

From the figure, OB = OC ( radius of a circle) ∴ OBC is an isosceles triangle i.e ∡OBC =  ∡OCB In ▲OBC, x + 64o + 64o  = 180o (sum of interior angles of a triangle) or, x = 180o - .....

32. Find the area of the given figure.

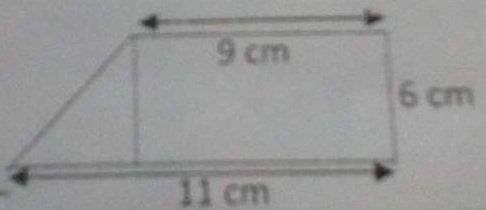
The above figure consists of two shapes: A triangle at left and a rectangle at right. First for the triangle: Base ( b ) = 11 - 9 = 2 cm. Height ( h ) = 6 cm. Area of the triangle = 1/2 x b x h               .....

33. What is a variable motion? Explain it with an example.

.....

34. Find the area of the given quadrilateral ABCD in which ∡DBC = 60o, AB = AD, BC = CD = 8 cm and AC = 12 cm.

.....

35. In the figure, I is the centre of the circle. PM and PN are two circle. PM and PN are two tangents. If ∡MIN =158⁰, find ∡MPN.

.....

36. Write down the difference between vector quantity and scalar quatity with example.

.....

37. In the given diagram, ABCD is a parallelogram. AB = 8 cm, BF =5 cm ∡ADC = 100⁰ and ∡CBF = 20⁰. Find the area of parallelogram ABCD.

 

.....

38. Why is speed called a scalar quantity?

.....

39. What are the various effects of the force? Explain.

.....

40. Define:
a. Velocity                     b. Uniform-velocity
c. Variable-velocity       d. Objects at rest
e. Object in motion

.....

41. How does friction occur?

.....

42. Why can the moon not escape from the earth?

.....

43. What is relative velocity?

.....

44. In the given figure, ABCD is a kite. If the diagonals AC and BD intersect each other at O making 90o, find area of the kite ABCD.

 

.....

45. Find the volume of the figure given below.

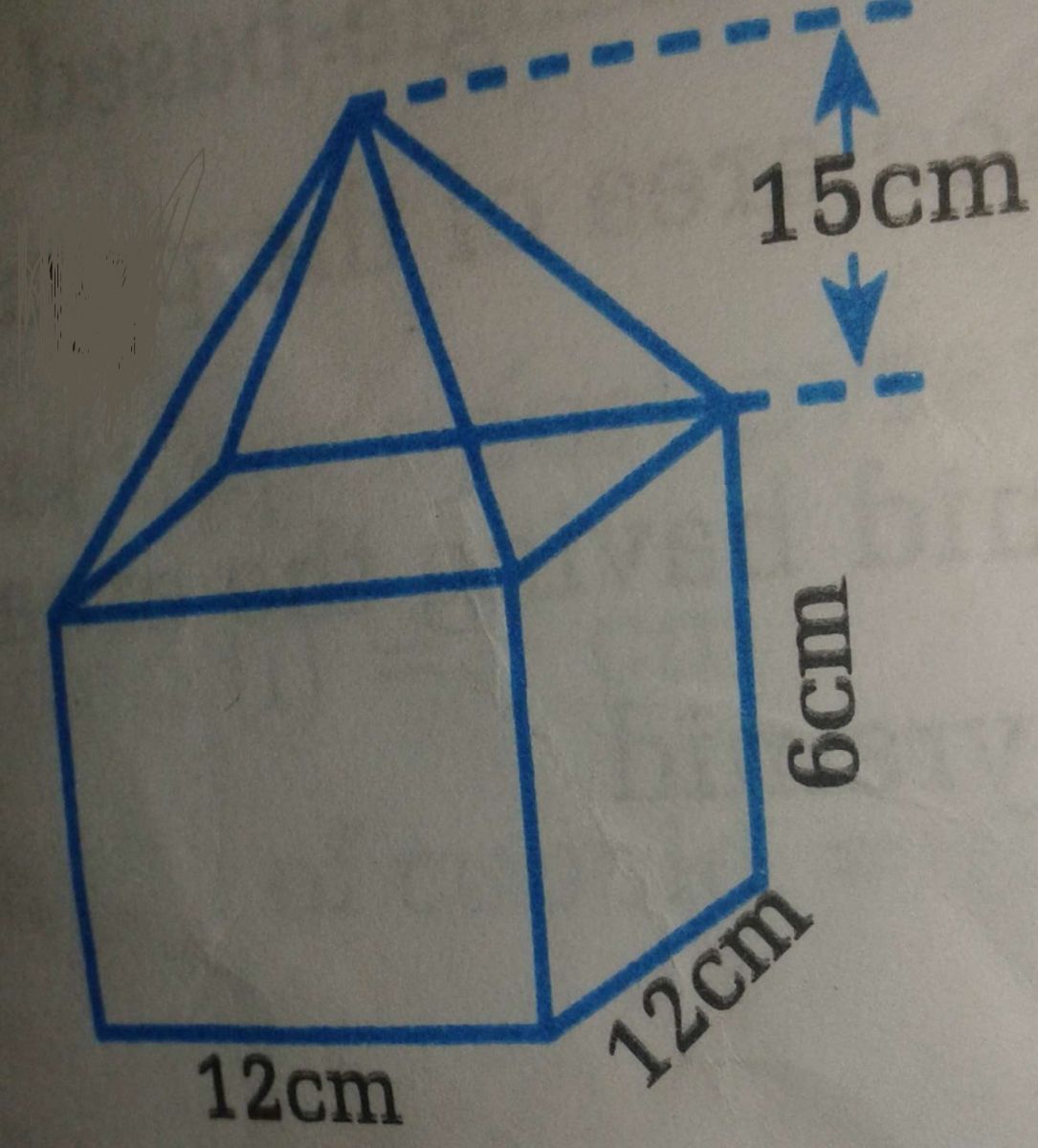
Height of pyramid ( hp ) = 15 cm. Height of cuboid ( hc ) = 6 cm Length of cuboid ( lc ) = breadth of cuboid ( bc ) = 12 cm  Volume of upper pyramid ( Vp ) = ( 1 / 3 ) x length x breadth       .....

46. What are rest and motion?

.....

47. The volume of water in a measuring cylinder is 100cm3. On immersing a brick compeletely in water, the level rises to 120cm3. Calculate the volume of the brick.

.....

48. In the given figure, two circles are intersecting at M and N. PQ and RS pass through M. If R, P, S and Q are joined to N, prove that ∠PNR =∠SNQ.
 
 

.....

49. Explain an experiment to measure the volume of an irregular solid.

.....

50.  Line segments TQ and TR are equal in length. Prove that PQ = SR and PR = QS.

.....