Students and Teachers Forum

1. In a survey of 100 people, 65 read Kantipur, 45 read Gorkhapatra, 40 read Himalaya times, 25 read Kantipur as well as Gorkhapatra, 20 read  Kantipur as well as Himalaya times, 15 read Gorkhapatra as well as Himalaya times. If each person of a survey reads at least one type of newspaper, find how many people read all three types of newspapers.

Let,       Total number of people surveyed, n(U) = 100       No. of people who read Kantipur, n(K) = 65       No. of people who read Gorkhapatra, n(G) = 45       No. of people who read .....

2. Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).

Given, n(A) = 20, n(B) = 28 and n(A ∪ B) = 36,  n(A ∩ B)= ? Using the formula n(A ∪ B) = n(A) + n(B) - n(A ∩ B).  Or,  n(A ∩ B) = n(A) + n(B) - n(A ∪ B)                 .....

3. In a school, all students play either table tennis or chess or both. 175 play table tennis, 143 play chess and 106 play both games. Draw a venn diagram to illustrate the above information and find 
(i)    the number of students who play table tennis only
(ii)   the number of students who play chess only
(iii)  the total number of students in the school.

Let,       No. of students who play table tennis, n(T) = 175       No. of students who play chess, n(C) = 143       No. of students who play both, n(T∩C) = 106       No. of students who .....

4. If n (A) = 65, n (B) = 50, n (C) = 35, n (A∩B) = 25, n (B ∩ C) = 20, n (C ∩ A ) = 15, n (A ∩ B ∩ C) = 5 and n(U) = 100. Represent all the information in a venn-diagram and find no(A), no(B), no(C) and n(A U B U C)ˈ, 

Given, n (A) = 65 n (B) = 50 n (C) = 35 n (A∩B) = 25 n (B ∩ C) = 20 n (C ∩ A ) = 15 n (A ∩ B ∩ C) = 5 n(U) = 100 no(A) = ? no(B) = ? no(C) = ? n(A U B U C)' = ?   Representing in Venn - diagram: From venn .....

5. 45 people were asked whether they liked to drink lemon tea or milk tea. 15 liked lemon tea, 32 liked milk tea and 7 did not like either. How many like both lemon tea and milk tea?
How many of the like 
         (a) lemon tea only 
         (b) milk tea only
Represent all the information in venn-diagram.
 

Let,      Total number of people asked, n(U) = 45      Number of people who like to drink lemon tea, n(L) = 15      Number of people who like to drink tea, n(M) = 32      Number of people .....

6. On the occasion of “International Tuberculosis Day” a sample of people randomly selected were asked about the causes of Tuberculosis disease in order to study people’s awareness of this disease. Among the respondents, 110 people said ‘alcohol’, 75 said ‘smoking’ and 60 people answered ‘diet’ as a cause. Again out of them there were 25 people who said both alcohol and smoking, 10 said smoking and diet and 10 said alcohol and diet, and 5 of them indicated all the three causes.Represent this data in a Venn diagram and find the number of people,
(a)    who mentioned alcohol and smoking only.
(b)    who mentioned alcohol and diet only.
(c)    who mentioned alcohol as the only cause.

Let, A, S and D represent Alcohol, Smoking and Diet. Then,     Number of people who said alcohol, n(A) = 110 Number of people who said smoking, n(S) = 75 Number of people who said diet, n(D) = .....

7. In a group of 260 persons, 130 read Kantipur but not Annapurna post, 168 read Kantipur and 10 read neither of them. Find the number of persons 
(a) who read Kantipur and  Annapurna post both 
(b) who read Annapurna post but not Kantipur 
(c) Represent the above information in venn-diagram.
 

Let,      Total number of people, n(U) = 260       No. of people who read Kantipur but not Annapurna post, no (K) = 130       No. of people who read Kantipur, n(K) = 168       No. of people .....

8. Out of 100 students in final examination of X class, 75 passed in Mathematics, 65passed in Nepali and 10 failed in both subjects. Using venn-diagram, find the number of students who passed in
(a) both subject
(b) Mathematics only
(c) Nepali only.

Let,      Total number of students, n(U) = 100      No. of students who passed in Mathematics, n (M) = 75      No. of students who passed in Nepali, n(N) = 65      No. of students who .....

9. Among 100 students of a school, 85 students like Arithmetic, 65 liked geometry and 10 did not like both, 
(a) How many liked both? 
(b) How many liked geometry only? 
(c) Show the above information in ven-diagram.
 

Let,       Total number of students, n(U) = 100       No. of students who like Arithmetic, n(A) = 85       No. of students who like Geometry, n(G) = 65       No. of people who do not like .....

10. In an examination, 35% of students passed in Nepali only and 25% passed in Maths only. If 20% of students failed in both subjects, 
 (i)    What percent of students passed in both subjects?
(ii)    What percent of students passed in Maths?
 

Let, N and M denote the sets of students passed in Nepali and Maths respectively. Venn-diagram: Then,           n(U) = 100%           no(N) = .....

11. If n(A) = 65, n(B) = 50, n(C) = 35, n(A∩B) = 25, n(B∩C) = 20, n(C∩A) = 15, n(A∩B∩C) = 5 and n(U) = 100, find the value of n(A∪B∪C)ˈ.
 

Here, n(A) = 65                     n(B) = 50 n(C) = 35                     n(A∩B) = 25 n(B∩C) = 20        .....

12. Let A, B, C be the subsets of the universal set U. Given n (U) = 100, n (A) = 48, n (B) = 39, n (C) = 33, n (A ∩ B) = 12,
n (B ∩ C) = 9, n (C ∩ A) = 13 and n (A ∩ B ∩ C) = 3, present the above information in the venn diagram and find no (A ∩ B),
no (B ∩ C) and no (B). 

Given, n (U) = 100                n (A) = 48 n (B) = 39                  n (C) = 33 n (A ∩ B) = 12          n (B ∩ C) = 9 n (C .....

13. Some students were asked whether they like to have a picnic to Godavari, Sundarijal or Balaju. The result was 60% Godavari, 45% Sundarijal and 20% Balaju, 15% Godavari and Sundarijal, 12% Sundarijal and Balaju, 10% Balaju and Godavari and 7% none of them. If 15 students like all three places, how many students were asked? 

Let, Number of students who like Godavari, n(G) = 60% Number of students who like Sundarijal, n(S) = 45% Number of students who like Balaju, n(B) = 20% Number of students who like Godavari and Sundarijal, n(G∩S) = 15% Number of students who .....

14. If n(∪) = 100, n(A) = 60, n(B) = 75 and n(A ∩ B) = 40, find the value of n(A∪B)ˈ. 

Given,  n(∪) = 100 n(A) = 60  n(B) = 75  n(A ∩ B) = 40  n(A∪B)ˈ = ? We know, n(A ∪ B) = n(A) + n(B) – n(A ∩ B)                     = 60 + 75 .....

15. In a group of students, 20 study Accountancy, 20 study Mathematics, 18 study History, 7 study Accountany only, 10 study Mathematics only, 6 study Accountancy an d Mathematics only and 3 study Mathematics and History only. 
(i) Represent the above information in venn-diagram 
(ii) How many students are there altogether? 
 

Let,          Number of students who study Accountancy, n(A) = 20          Number of students who study Maths, n(M) = 20          Number of students who study History, n(H) .....

16. Complete the formula, n(A ∪ B) = n0(A) + n0(B) ………?

This is the formula to find the value of  n(AUB). So,  n(A ∪ B) = n0(A) + n0(B) + n(A ∩ .....

17. In a certain survey, 73% of the people liked to listen radio, 85% liked to watch the television and 65% liked to listen radio as well as to watch the television. If 210 people neither like to listen radio nor to watch the television, how many people have taken part in the survey. Show the above information in a venn-diagram. 

We have given,        Percentage of people who like to listen radio, n(R) = 73%        Percentage of people who like to watch TV, n(T) = 85%        Percentage of people who like to listen .....

18. Write the shaded portion of given Venn-diagram as union of two sets.

The set notation for the shaded portion of the given Venn-diagram is (A – B) ∪ (B – A) .....

19. In the survey of a community, 45% of the people like Dashain festival, 65% like Tihar festival and 20% like both festival. What is the percentage of people who do not like both festivals?

Let D = Dashain and T = Tihar Given, Percentage of people who liked Dashain, n(D)                 = 45% Percentage of people who liked Tihar, n(T)                .....

20. In a class of some students, 80% selected science, 60% selected mathematics and 50% selected both the subjects. If 12 students did not select any of the given two subjects, find the number of students in the class. Also draw a Venn-diagram to represent above information.

Let S = Science and M = Mathematics Then, Percentage of students who selected science, n(S) = 80%  Percentage of students who selected mathematics, n (M) = 60%  Percentage of students who selected both the subjects, n (S ∩ .....

21. In a survey conducted among some people of a group, it was found that 40% of them liked literature, 65% of them liked music and 10% of them liked none.
i. Represent the above information in a Venn-diagram.
ii. If there were 30 people who liked both of them, find the number of people participated in the survey.

Let L and M be the set of people who liked literature and music respectively.  Then, Percentgae of people who liked literature, n (L) = 40%  Percentage of people who liked music, n (M) = 65%  Percentage of people who liked none, .....

22. If n (U) = 300, n (A) = 150, n (B) = 180 and n (A ∩ B) = 70, then represent the above information in a venn-diagram and find no(A), no(B), n (A U B) and n(A U B)ˈ. 

Given,       n (U) = 300       n (A) = 150       n (B) = 180        n (A ∩ B) = 70 Venn-diagram : From Venn-diagram,        no(A) = 80       .....

23. In a survey, it is found that 186 families used filter water, 142 families used boiled water and 102 families used both types of water. How many families used at least one type of water?

Let,        Number of families that use filter water, n(F) = 186        Number of families that use boiled water, n(B) = 142        Number of families that use both types of water, n (F .....

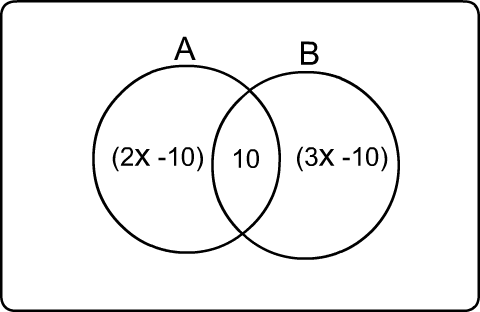
24. SIn the given Venn- diagram, n (A ∪ B) = 90, find n (A).

Here, n (A ∪  B) = 90  n (A) = ? From the given Venn-diagram,  n (A ∪ B) = no(A) + n(A∩B) + no(B)  Or, 90 = 2x – 10 + 10 + 3x – 10  Or, 90 = 5x – 10  Or, 5x = 100  Or, x = .....

25. In a group of people, 20 speak Nepali, 18 speak English, 21 speak Hindi, 7 speak only Nepali, 10 speak only English, 6 speak Nepali and Hindi only and 3 speak English and Nepali only. Use the Venn-diagram and find
i. The number of people who speak all three languages.
ii. The total number of people in the group.

Let N, E and H be the set of people who speak Nepali, English and Hindi respectively.  Then, Number of people who speak Nepali, n (N) = 20  Number of people who speak English, n (E) = 18  Number of people who speak HIndi, n (H) = .....

26. Out of 120 students appeared in an examination the number of students who passed in mathematics only is twice the number of students who passed in science only. If 50 students passed in both subjects and 40 students failed in both subjects then,
(i)    Find the number of students who passed in Mathematics.
(ii)   Find the number of students who passed in Science.
 

Let , M and S represent the set of students who passed in Mathematics and Science respectively.  According to the question, Total number of students appearing in exam, n(U) = 120 Number of students who passed in both subjects, n(M∩S) .....

27. Define singleton set with example.

A set having only one element is called singleton set. It is also known as a unit set. A singleton set is denoted by . Example: The set of even prime numbers. (There is only one even prime number i.e. .....

28. In a test of two subjects, 70% of the students passed in English and 50% passed in mathematics, whereas 5% could not pass in any subject. If 45 students passed in both the subjects, how many students failed in both the subjects?

Let M and E be the set of students who passed in mathematics and English respectively.  Then, Total percentage of students, n (U) = 100%  Percentage of students who passed in English, n (E) = 70%  Percentage of students who passed in .....

29. If P, Q, R are subsets of U, where n(P) = 100, n(Q) = 90, n(R) = 110, n(P ∩ Q) = 60, n(Q ∩ R) = 40, 
n(P ∩ R) = 45 and, n(P∪ Q ∪R) = 180. Find n(P ∩ Q ∩ R).
 

Here, P, Q, R are subsets of U. n(P) = 100, n(Q) = 90, n(R) = 110, n(P ∩ Q) = 60, n(Q ∩ R) = 40,  n(P ∩ R) = 45 and, n(P ∪ Q ∪ R) = 180. n(P∩ Q ∩ R) = ? We know, n(P∪Q ∪R) = n(P) + n(Q) + n(R) – n(P .....

30. In a survey of 120 people, it was found that 90 people liked Kantipur daily, 70 liked Himalayan Times daily. If all the people like at least one of the two newspapers, find the number of people who liked both the newspapers. Also show the above information in a Venn-diagram.

Let K and H be the set of people who liked Kantipur and Himalayan Times respectively.  Then, Total number of people surveyed, n (U) = 120 Number of people who like Kantipur daily, n (K) = 90  Number of people who like HImalayan Times, n .....

31. Among 120 people, 80 drink tea and 40 drink coffee. 20 of them drink neither tea nor coffee. Answer the following questions with the help of a Venn-diagram. 
i.   How many of them drink tea only?
ii.  How many of them drink only one out of these two?
 

Let T and C be the set of people who drink tea and coffee respectively.  Then, Total number of people, n (U) = 120  Number of people who drink tea, n (T) = 80  Number of people who drink coffee, n (C) = 40  Number of people who .....

32. In a class of 25 students, 17 favoured volleyball, 15 favoured basketball and 10 favoured both games. Find the number of students who didn’t like any of the sports.

Let V denotes the set favouring volleyball and B denotes the set favouring basketball. Then, total number of students, n(U) = 25 Number of students who favoured volleyball, n(V) = 17 Number of students who favoured basketball, n(B) = 15 Number of .....

33. In a competition, a school awarded medals in different categories. 36 medals in dance, 12 medals in dramatics and 18 medals in music. If these medals went to a total of 45 persons and only 4 persons got medals in all the three categories, how many received medals in exactly two of these categories?

Let, A = set of persons who got medals in dance. B = set of persons who got medals in dramatics. C = set of persons who got medals in music. Then, Number of people who got medals in dance, n(A) = 36 Number of people who got medals in dramatics, .....

34. In a survey, it was found that the ratio of people liking arithmetic and algebra is 9:8. If 25% of people liked both, 80 liked none of these and 20% liked arithmetic only, find the total number of people participating in the survey.

Let, R be the number of people who like arithmetic and L be the number of people who like algebra. Here the ratio of people liking arithmetic to algebra, R:L = 9: 8. If x is any constant, then,  Number of people who like arithmetic, n(R) = .....

35. If A ⊂ B, n(A) = 50 and n(B) = 80, what is the possible value of n(A∩ B)?

Given, n(A) = 50 and n(B) = 80, Possible value of n(A∩ B) = ? Since A ⊂ B, all the elements of set of A is also the elements of B. So, n(A∩ B) = n(A)                      .....

36. If P, Q, R are subsets of U, where n(P) = 150, n(Q) = 80, n(R) = 100, n(P ∩ Q) = 90, n(Q ∩ R) = 30, 
n(P ∩ R) = 45 and, n(P∪ Q ∪R) = 180. Find n(P∩ Q ∩ R).
 

Here, P, Q, R are subsets of U. n(P) = 150, n(Q) = 80, n(R) = 100, n(P ∩ Q) = 90, n(Q ∩ R) = 30,  n(P ∩ R) = 45 and, n(P∪ Q ∪R) = 180. We know, n(P∪ Q ∪R) = n(P) + n(Q) + n(R) -n(P ∩ Q) - n(Q ∩ R) - n(P .....

37. In a survey organized by an institution regarding the causes of HIV, 110 said it is transferred by unprotected sex, 75 said it is by infected syringes and 60 said it is by infected parent who can infect their babies. Similarly, 25 said it is both by infected syringes and infected parents, 10 said it is spread by unprotected sex and infected parents, and 5 believe in all three factors. If all the people surveyed believe in at least one of the factors,
a) Show the information in a Venn – diagram.
b) How many people were surveyed?
c) How many people said that it is caused by infected syringes only?
 

Let A be the people who blieve that HIV is spread by unprotected sex, B be people believing that HIV spreads through syringes and C be people who belive that HIV spreads through affected parents. a) Venn-diagram. From Venn diagram, b) Total .....

38. There are 35 students in art class and 57 students in dance class. Find the number of students who are either in art class or in dance class,
i.  When two classes meet at different hours and 12 students are enrolled in both activities.
ii. When two classes meet at the same hour. 

Let A be the set of students in art class. B be the set of students in dance class. Then, Number of students in art class, n(A) = 35 Number of students in dance class, n(B) = 57 Now, (i) When 2 classes meet at different hours, n(A ∪ B) = .....

39. In a venn-diagram given below if E, M and N be the set of students liking to read English, Mathematics and Nepali respectively. If n (E U M U N) = 100%, find the percentage of the students liking to read all three subjects. 
 

Let x be the number of students who like to read all three subjects. Then, n(E ∩ M ∩ N) = x We know,           n(U) = n(E) + n(M) + n(N) – n(E ∩ M) - n(E∩ N) - .....

40. Some people were asked whether they liked to visit Pokhara or Lumbini. The result was 48% liked to visit Pokhara only, 45% liked to visit Lumbini only and 5% liked both Pokhara and Lumbini to visit,
(a) Represent the above information in venn-diagram.
(b) If 2940 people visited at least one of the places, find the number of people who visited Pokhara only.

Let,       Percentage of people who like to visit Pokhara only, no(P) = 48%       Percentage of people who like to visit Lumbini only, no(L) = 45%       Percentage of people who like to visit both, .....

41. 32 teachers in a school like either milk or curd or both. Out of them, 8 like both milk and curd. The ratio of the number of teachers who like milk to the number of teachers who like curd is 3:2. Find
(i) How many teachers like milk?
(ii) How many teachers like curd only?

Let, M and C represent the set of teachers who like milk and curd respectively. Then, Total number of teachers, n(U) = 32 Number of teachers who like both milk and curd. n(M∩C) = 8 Ratio of number of teachers who like milk to curd = 3:2 Soi, if .....

42. If P is the set of factors of 8 and Q is the set of factors of 12, draw a Venn diagram illustrating the relation between P and Q and find the value of n(P∩Q).

Here, P = {1, 2, 4, 8}  Q = {1, 2, 3, 4, 6, 12}   Representing P and Q in the Venn diagram,  Now using the Venn diagram,  P∩Q = {1, 2, 4} So, n(P∩Q) = .....

43. In a school, all students play either football or volleyball or both. 300 play football, 250 play volleyball and 110 play both the games.
Using Venn-diagram find
(i) the number of students who play football only
(ii) the number of students who play volleyball only
(iii) the total number of students in the school.

Let,       Number of students who play football, n(F) = 300       Number of students who play volleyball, n(V) = 250       Number of students who play both games, n(F∩V) = 110       .....

44. From the given Venn-diagram, find the value of x.

Here, For the given sets in terms of percentage,  n(U) = 100%  In the given Venn-diagram,  n (U) = no(A) + n(A∩B) + no(B) Or, 100% = 50% + 20% + 20% + x  Or, 100% = 90% + x  Or, x = 100% – 90% Or, x = 10% ∴ .....

45. Following are the findings in a study done on the earth environment:
The temperature on the earth is increasing. The number of amphibians is decreasing. Human beings are suffering from cataract and skin cancer. Answer the following on the basis of the above facts:
a.    What is the cause of the above findings?
b.    What is to be done to be safe from the above conditions?
c.    Write down its more harmful effects to the human health.
d.    What happens to the environmental temperature at this condition?

a.  The main cause of the above finding is depletion of the ozone layer. b.  The production of chlorofluorocarbon (CFCs), methyl chloroform, carbon tetrachloride, nitrogenous fertilizers and fossil fuel should be .....

46. Write short notes on:
a.    Nebular hypothesis
b.    Tidal hypothesis

a.    Nebular hypothesis According to Nebular hypothesis, the sun and the planets were formed from a large whirling cloud of hot gases and dust. When the cloud cooled and grew smaller, it began to spin faster. As the surface of the .....

47. 1.    Write the name of era and its duration for each of the following incidents.
        a.    Invertebrates originated in sea
        b.    Evolution of human beings
        c.    Evolution and extinction of dinosaur
 

a.    Invertebrates originated in sea Era: Proterozoic era Duration: 2500 -542 million years ago b.    Evolution of human beings Era: Cenozoic Duration: 65 million years ago to till now c.    Evolution .....

48. Green house gases cause global warming, why?

Some gases such as CO2, CH4, and N2O etc. trap the solar radiation and prevent the escaping of heat radiation to outer space. Thus, causes rapid increases in the earth temperature i.e. global .....

49. Write its two effects and two preventive measures of water pollution in points.

The effects of water pollution are: i.    It causes several water borne communicable diseases. ii.    It harms the growth of aquatic animals. The preventive measures for water pollution for: i.    The .....

50. Mention three measures of conservation and management of water.

The measures of conservation and management of water are: i.    Programmes must be conducted to protect sources of water. ii.   Polluted water must be treated, surface water must be stored and excess water must be used .....