Students and Teachers Forum

1. The base of a rectangular pyramid is 8 cm long and 5 cm broad. If the height of the pyramid is 6 cm, find the volume of the pyramid. 

Solution: Here,        Length of the base of rectangular pyramid (l) = 8 cm        Breadth of the base of rectangular pyramid (b) = 5 cm        Area of the base of the pyramid (A) = .....

2. Find the volume of a closed regular pyramid of which the base is a square of side 8 cm and height 15 cm. 

Solution: Given,           Side of the square base (a)     = 8 cm. Now,           Area of the base (A)     = a2               .....

3. A pyramid having vertical height 8 cm is placed on the top of a cubical object. If the measure of the side of the cube is 12 cm, find the total volume of the combined object.

Solution: Here,          The length of the base of the pyramid = the side of the cube = a = 12 cm          The height of the pyramid = h = 8 cm. Now,          The volume of .....

4. A square based pyramid having total surface area 800 cm2 has the length of base 16 cm. find the lateral surface area and the volume of the pyramid.

Solution: Here,          Lngth of the base of pyramid (a) = 16 cm          Let, l and h be the slant height and height of the pyramid. We have,         TSA of the pyramid = 800 .....

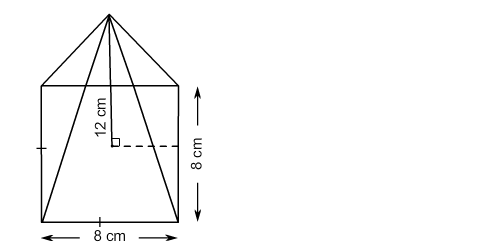
5. The height of a square pyramid having the area of its base 64 cm2 is 12 cm. Find the volume of the pyramid. 

Solution:          Height of the pyramid (h) = 12 cm         Area of the square base (A) = 64 cm2 We know,          Volume of the pyramid (V) = 1/3⨉ Area of base ⨉ .....

6. Find the total surface area of the cone having the circular base of diameter 8 cm and height 3 cm.

Solution: Given,          Diameter of the base (d) = 8 cm          Radius of the base (r) = d/2 = 8 cm/2 = 4 cm          Height of the cone (h) = 3 cm. According to .....

7. Find the volume of the cone having radius 7 cm and height 9 cm.

Solution: Given,         Radius = r = 7cm        Height = h = 9cm Now, The volume of the cone is given by,        Volume= 1/3 πr2h     .....

8. Find the curved surface area of the cone having the circular base of radius 5 cm and height 12 cm.

Solution: Given, Radius of the base (r) = 5 cm     Height of the cone (h) = 12 cm According to Pythagoras theorem, Slant height of the cone (l) = √(r2+ h2 )                .....

9. Find the total surface area of the cone having the circular base of diameter 10 cm and height 24 cm.

Solution: Given,        Diameter of the base (d) = 10 cm        Radius of the base (r) = d/2 = 10 cm/2 = 5 cm        Height of the cone (h) = 24 cm.        According to .....

10. A pyramid has the base rectangle of area 35 cm2. If the area of the triangular faces along the length and breadth of the base of pyramid are 20.8 cm2 and 16.4 cm2, find the total surface area of the pyramid. 

Solution: Given,         Area of the base of pyramid (A) = 35 cm2         Area of the triangular faces along the length = 20.8 cm2         Area of 2 triangular faces along the length (Al) .....

11. Find the total surface area of the cone having the circular base of radius 5.6 cm and slant height 10 cm.

Solution: Given,         Radius of the base (r) = 5.6 cm         Slant height of the cone (l) = 10 cm. We know,         Total surface area of the cone (TSA) = πr (r + l)     .....

12. If a square based pyramid has a slant height 'l' and vertical height 'h', write down the formula to a length of the base.

Solution: Here,         Slant height = l,         Vertical height = h,         Length of base = a = ? Now,     The length of the base of the pyramid is given by,     .....

13. Find the curved surface area of the cone having the circular base of diameter 3 cm and slant height 5 cm.

Solution: Given,         Diameter of the base (d) = 3 cm         Radius of the base (r) = d/2 = 3 cm/2 = 1.5 cm         Slant height of the cone (l) = 5 cm. We know, Curved surface area .....

14. Find the curved surface area of the cone having the circular base of diameter 10 cm and slant height 13 cm.

Solution: Given,       Diameter of the base (d) = 10 cm       Radius of the base (r) = d/2 = 10 cm/2 = 5 cm       height of the cone (l) = 13 cm. We know, Curved surface area of the cone (CSA) = .....

15. Find the curved surface area of the cone having the circular base of radius 8.4 cm and slant height 15 cm.

Solution: Given, Radius of the base (r) = 8.4 cm Slant height of the cone (l) = 15 cm We know, Curved surface area of the cone (CSA) = πrl                     = 22/7 X 8.4 .....

16. The base of a pyramid is a rectangle of 8 cm long and 6 cm broad. If the area of the triangle along the length and breadth of the rectangle base are 20 cm2 and 15 cm2 respectively, find the total surface area of the pyramid. 

Given,         Length of the base (l) = 8 cm         Breadth of the base (b) = 6 cm. Area of the base (A1)   = lb                         .....

17. A cone has vertical height and slant height 24 cm and 25 cm respectively. Find the radius of the cone.

Solution: Given,        Height = h = 24cm        Slant height = l = 25cm.        Radius = r =? We know,           Radius of the cone .....

18. The volume of a rectangular pyramid is 230 cm3. If the area of its rectangular base is 115 cm2, find the height of the pyramid. 

Solution: Here,          Volume of the pyramid (V) = 230 cm3           Base area of the pyramid (A) = 115 cm2 We know,          Volume of the pyramid (V)    .....

19. Find the total surface area of a square-based pyramid in which the area of the base is 48 cm2 and the area of each triangular face is 24.5 cm2

Solution: Here,         Area of base (A1) = 48 cm2        The area of each triangular face (A2) =24.5 cm2 Now,  Total surface area of a pyramid is given by,   .....

20. A triangular prism has base area and perimeter x cm2 and y cm respectively. If the height of the prism is z cm, what is the total surface of prism?

Solution: We have, The total surface area of prism is given by, TSA = area of 2 triangular base + Perimeter of base × Height of prism         = (2x +yz) .....

21. The height of a square-based pyramid having the area of its base 81 sq. meters is 18 meters. Find the volume of the pyramid.

Solution: The volume of prism is given by, Volume = 1/3 × Area of square base × height of prism               = 81cm2×18cm /3               = 486 .....

22. The Lateral Surface Area of  an equilateral triangle base pyramid is 540 cm2 and slant height is 30 cm. Calculate the volume of the pyramid.

Let, a be the base of pyramid, l be the slant height and h be the height of  it. We know, Lateral Surface Area of pyramid = 4 ⨉ Area of one triangle  Or, 540 = 4⨉ 1/2 ⨉ 30 ⨉ a  Or,  a = 12 cm. Now, (slanted .....

23. The square based pyramid having total surface area 384 cm2 has the length of base 12 cm. find the volume of the pyramid.

Solution:        The length of the base of the pyramid (a) = 12 cm Here,          Total surface area of the pyramid = 384 cm2 Or,    a2 +2ah = 384 Or,    122 + 2×12×h = .....

24. The given figure is a square based pyramid in which vertical height is 8 cm and length of the base is 12 cm. Find its total surface area.

We have given, Base of pyramid = a =12cm. Height of pyramid  = h = 8cm. We know,      l2 = (a/2)2 + h2  or,l2 = 62 + 82 = 102  Therefore, slanted height (l) = 10 cm. We know,        .....

25. Find the total surface area of the cone having the circular base of diameter 10 cm and slant height 13 cm.

Solution: Given,         Diameter of the base (d) = 10 cm         Radius of the base (r) = d/2 = 10 cm/2 = 5 cm         Slant height of the cone (l) = 13 cm. We know,       .....

26. Find the area of the triangular surfaces of the given pyramid.

Solution: Here,      AM = MB = ½ ⨉ 6 cm = 3 cm      BN = NC = ½ ⨉ 8.4 cm = 4.2 cm      OM = 5.8 cm. In right angled triangle OMB, OB = √(OM2+ MB2  )       = .....

27. Find the volume of the given pyramid.

Solution: Here,        Height of right angled triangular base (h) = 8 cm        Base length of the triangular base (b) = 6 cm Now,          Area of triangular base (A) = ½⨉ .....

28. Find the volume of the given pyramid.

 

Solution: Here,        Length of the base of pyramid (l) = 8 cm        Breadth of the base of pyramid (b) = 8 cm        Area of the base of the pyramid (A) = lb         .....

29. What height of the prism shown in the figure makes its volume 48 cm3?

Solution:           Let, a = AB = 3cm , b = BC = 4cm. Here, the volume of the prism=480 cm3 or,    Area of base ⨉  height = 480cm3  or,      abh2 = 480cm3  or, .....

30. The given diagram is a solid prism of triangular base. If the volume of the prism is 480 cm3, find its height.

Solution:       Let, c=10cm , a=8 cm . Now,        b = c2-a2         = 102-82         = 6 cm. Here, the volume of the prism = 480 cm3  or,    Area .....

31. Find the surface area of a square base pyramid with base length measuring 24 cm and slant height measuring 13 cm.

Solution: Given,         Length of the base (a) = 24 cm         Area of the square base (A)     = a2                           .....

32. Find the curved surface area of the cone having the circular base of diameter 10 cm and height 24 cm.

Solution: Given,         Diameter of the base (d) = 10 cm         Radius of the base (r) = d/2 = 10 cm/2 = 5 cm         Height of the cone (h) = 24 cm, According to Pythagoras .....

33. Find the curved surface area of the cone having the circular base of diameter 10 cm and slant height 17.7 cm.

Solution: Given, Diameter of the base (d) = 10 cm Radius of the base (r) = d/2 = 10 cm/2 = 5 cm Slant height of the cone (l) = 17.7 cm We know, Curved surface area of the cone (CSA) = πrl            .....

34. The length of base of given square based pyramid is twice the height. If the volume of the pyramid is 288 cm3, find the measure of OP.

Solution: Let, h and a be the height and the length of base of the pyramid. Then,       a = 2h. Now,          The volume of the pyramid = 288 cm3 Or,   1/3×a2×h = 288cm3 Or,  .....

35. Find the area of triangular surface of given square based pyramid.

Solution: Here,        Slant height(h)=10cm and length of square base (a)=16cm. Now,         The area of triangular surfaces of pyramid is given by,              Are  .....

36. If a square based pyramid has a length of base 'a' and vertical height 'h', write down the formula to calculate slant height.

Solution: Given,         Length of base = a         Vertical height = h         Slant height = l =? We know,         The slant height of .....

37. Find the curved surface area of the cone having the circular base of diameter 28 cm and slant height 20 cm.

Solution: Given,       Diameter of the base (d) = 28 cm       Radius of the base (r) = d/2 = 28 cm/2 = 14 cm       Slant height of the cone (l) = 20 cm. We know, Curved surface area of the cone (CSA) = .....

38. Find the curved surface area of the cone having the circular base of diameter 42 cm and slant height 28 cm.

Solution: Given,          Diameter of the base (d) = 42 cm          Radius of the base (r) = d/2 = 42 cm/2 = 21 cm          Slant height of the cone (l) = 28 cm. We .....

39. The pyramid has a rectangular base of length 8 cm and breadth 6 cm. The slope edge of the pyramid has the length of 5 cm. Calculate the total surface area of the pyramid. 

Solution: Given,         Length of the base of pyramid (a) = 8 cm         Breadth of the base of pyramid (b) = 6 cm         Area of the base of pyramid (A)     = ab   .....

40. Calculate the total surface area of the given pyramid.

Solution: Given,         Length of the square base (a) = 10 cm         Area of the base of pyramid (A) =a2                             .....

41. Calculate the total surface area of the given pyramid. 

Solution: Given,       Length of the base of the pyramid (l) = 8 cm       Breadth of the base of the pyramid (b) = 6 cm       Area of the base of pyramid (A)     = lb       .....

42. Find the volume of the given pyramid. 

Solution: Here,           Length of the base of rectangular pyramid (l) = 12 cm           Breadth of the base of rectangular pyramid (b) = 7 cm           Area of the base of .....

43. Find the lateral surface area of the given triangular prism.

Solution: Let,        a=AB=16cm, b=AC=DF=20cm, c=CB, h=AD=45cm. Now,       In right angled triangle ABC,           c = b2-a2             .....

44. Find the volume of the given triangular prism.

Solution: Here,        The length of equilateral triangle (a) = 6cm        The height of prism(h) = 63cm. Now, the volume of the prism is given by,        Volume =Area of base ⨉ .....

45. Find the volume of given square based pyramid.

Solution: Here,         The height of the pyramid (h) = 8cm          The length of the square base(a) = 12cm. Now, we have formula, Volume of the pyramid is given by,         .....

46. In the given figure, the solid pyramid is of square based pyramid. The total surface area of the pyramid is 896 cm2 and the side of the square base is 14 cm. Find the straight height of it.

Let the slanted height be l and the vertical height be h. We know,      TSA = 4 ⨉ Area of triangle + Area of base square Or,4 ⨉ 1/2 ⨉ l  ⨉ 14 + 142 = 896, Or, 28l = 896 - 196 Or, l = 700 / 28 Or, l  .....

47. Find the total surface area of the given triangular prism.

Solution: Let,         a=AB=6cm, b=AC=DF=10cm, c=CB, h=AD=30cm Now,          In right angled triangle ABC,               c = b2-a2       .....

48. Calculate the total surface area of the given pyramid. 

Solution: Given,        Length of the base (a) = 10 cm       Area of the square base (A)     = a2                             .....

49. A pyramid having vertical height 12 cm is placed on the top of a square based cuboid-shaped solid object. If the base area of the cuboid is 10 cm2 and height is 9 cm, find the volume of the solid object.

Solution: Here,          The height of the pyramid (h1) = 12 cm          The area of the base of cuboid = the area of the base of pyramid = A = 10 cm2          The height of .....

50. Find the total volume of a cone with radius = 7 cm, and slanted height 25 cm.

Given,          Radius = r =7cm,          Slant height = l = 25cm. We know that,           (Slanted Height)2 = radius2 + (vertical height)2     Or, 252 = h2 + .....